Komputasi Numeris: Metode Muller (2)
Pendahuluan
Seperti yang telah dijelaskan sebelumnya, Metode Muller adalah sebuah metode pencarian akar persamaan dengan 3 titik aproksimasi. Seperti halnya Metode Newton-Raphson, metode Muller juga memiliki pendekatan deret Taylor untuk mencari seluruh akar dari sebuah persamaan polinomial seperti dibawah ini:
dapat kita temukan akar-nya satu demi satu menggunakan aturan deflasi sebagai berikut:
dimana x* adalah salah satu akar persamaan dari persamaan polinomial di atas.
Algoritma
Seperti sudah dijelaskan sebelumnya, berikut algoritma Muller:
1. Mulai
2. Metode Muller diawali dengan menentukan 3 variabel x0, x1 dan x2
3. Cari fx0, fx1 dan fx2

4. Cari koefisien a,b dan c persamaan kuadrat berikut menggunakan aturan Cramer
(selengkapnya dapat dibaca di sini)
5. Cari nilai x3 dengan formula:
6. Hitung error = |x3-x2|
7. Rubah koefisien x0=x1, x1=x2 dan x2=x3.
8. Jika error masih lebih besar dari toleransi error yang diberikan, ulangi langkah 3 dan jika tidak, maka tampilkan x3 sebagai akar persamaan.
9. Selesai
Algoritma di atas dapat dimodifikasi untuk mencari akar-akar dari sebuah polinomial menggunakan formula:
Contoh:
Carilah akar-akar polinomial berikut dengan menggunakan metode Muller:
Perhatikan tabel excel berikut:
Keterangan:
Pencarian akar berikutnya
Pencarian akar berikutnya dilakukan dengan mengganti koefisien a4, a3, a2, a1 dan a0 dengan b4, b3, b2, b1 dan b0 seperti ditunjukkan pada tabel excel sebagai berikut:
Proses ini dapat diulang untuk pencarian akar ke 3 dan 4.
Menulis kode program
Setelah kita pahami algoritma Metode Muller di atas, saatnya menulis kode program. Berikut kode programnya.
//Menulis Identitas Program
/*
Program mencari akar polinomial dengan Metode Muller
Haruno Sajati, S.T., M.Eng.
Prodi Teknik Informatika
Sekolah Tinggi Teknologi Adisutipto
*/
//Deklarasi Header
#include<iostream.h>
#include<math.h>
//Fungsi Utama
void main()
{
//Deklarasi variabel
float koeff[10],koefg[10],x0,x1,x2,x3,error,fx0,fx1,fx2,a,b,c,d;
int j,k,iterasi;
//Inisialisasi persamaan
koeff[4]=1;
koeff[3]=2.8;
koeff[2]=-0.38;
koeff[1]=-6.3;
koeff[0]=-4.2;
for (k=4;k>=1;k--)
{
//Inisialisasi aproksimasi, error dan iterasi
x0=-0.5;
x1=0;
x2=0.5;
cout <<"Mencari akar ke : " << k << endl;
error=1;
iterasi=0;
//Lakukan perulangan jika error > toleransinya
while (error>0.00001)
{
//Mencari fx0, fx1 dan fx2
fx0=0;
for (j=4;j>=1;j--)
{
fx0=fx0+(koeff[j]*(pow(x0,j)));
}
fx0=fx0+koeff[0];
fx1=0;
for (j=4;j>=1;j--)
{
fx1=fx1+(koeff[j]*(pow(x1,j)));
}
fx1=fx1+koeff[0];
fx2=0;
for (j=4;j>=1;j--)
{
fx2=fx2+(koeff[j]*(pow(x2,j)));
}
fx2=fx2+koeff[0];
//Mencari koefisien a,b dan c persamaan fiting kuadrat
c=fx2;
b=(((x0-x2)*(x0-x2)*(fx1-fx2))-((x1-x2)*(x1-x2)*(fx0-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));
a=(((x1-x2)*(fx0-fx2))-((x0-x2)*(fx1-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));
d=(b*b)-(4*a*c);
//Mencari x3 (aproksimasi berikutnya
if (b<0)
{
x3=((-2*c)/(b-sqrt(d)))+x2;
}
else
{
x3=((-2*c)/(b+sqrt(d)))+x2;
}
//Mencari error
error=x3-x2;
if (error<0)
error*=-1;
//Perubahan aproksimasi
x0=x1;x1=x2;x2=x3;
iterasi++;
}
//Menampilkan output
cout << "Akar persamaan = " << x3 << endl;
cout << "Jumlah iterasi = " << iterasi << endl;
//Inisialisasi persamaan berikutnya
koefg[4]=0;
for(j=3;j>=0;j--)
{
koefg[j]=koeff[j+1]+(koefg[j+1]*x3);
}
for(j=4;j>=0;j--)
{
koeff[j]=koefg[j];
}
cout << "---------------------------------------" << endl;
}
}
Menjalankan Program
Berikut adalah eksekusi programnya:
Seperti yang telah dijelaskan sebelumnya, Metode Muller adalah sebuah metode pencarian akar persamaan dengan 3 titik aproksimasi. Seperti halnya Metode Newton-Raphson, metode Muller juga memiliki pendekatan deret Taylor untuk mencari seluruh akar dari sebuah persamaan polinomial seperti dibawah ini:
dapat kita temukan akar-nya satu demi satu menggunakan aturan deflasi sebagai berikut:
dimana x* adalah salah satu akar persamaan dari persamaan polinomial di atas.
Algoritma
Seperti sudah dijelaskan sebelumnya, berikut algoritma Muller:
1. Mulai
2. Metode Muller diawali dengan menentukan 3 variabel x0, x1 dan x2
3. Cari fx0, fx1 dan fx2

4. Cari koefisien a,b dan c persamaan kuadrat berikut menggunakan aturan Cramer
(selengkapnya dapat dibaca di sini)
5. Cari nilai x3 dengan formula:
6. Hitung error = |x3-x2|
7. Rubah koefisien x0=x1, x1=x2 dan x2=x3.
8. Jika error masih lebih besar dari toleransi error yang diberikan, ulangi langkah 3 dan jika tidak, maka tampilkan x3 sebagai akar persamaan.
9. Selesai
Algoritma di atas dapat dimodifikasi untuk mencari akar-akar dari sebuah polinomial menggunakan formula:
Contoh:
Carilah akar-akar polinomial berikut dengan menggunakan metode Muller:
Perhatikan tabel excel berikut:
- Kolom yang a4, a3, a2, a1 dan a0 (berwarna kuning) mewakili koefisien persamaan yang akan dicari.
- Kolom x0, x1 dan x2 (berwarna biru) mewakili nilai-nilai aproksimasi. Pada iterasi ke 0, nilai-nilai ini kita berikan sembarang yang penting tidak boleh sama. Perhatikan aturan/ formula Cramer di atas. Pembagi (penyebut) tidak boleh bernilai nol.
- Kolom x3 (berwarna merah) adalah nilai aproksimasi berikutnya. (Kita cari setelah seluruh kolom terisi)
- Kolom fx0, fx1 dan fx2 (berwarna pink), adalah nilai fungsi dari x0, x1 dan x2.
- Nilai a, b dan c (berwarna hijau) adalah koefisien-koefisien persamaan kuadrat Muller.
- Kolom b4, b3, b2, b1 dan b0 (berwarna orange) adalah persamaan deflasi dari persamaan sebelumnya atau persamaan yang terbentuk setelah satu akar ditemukan.
- Hasil-nya ditemukan pada iterasi ke 7 (diberi tanda merah)
Pencarian akar berikutnya
Pencarian akar berikutnya dilakukan dengan mengganti koefisien a4, a3, a2, a1 dan a0 dengan b4, b3, b2, b1 dan b0 seperti ditunjukkan pada tabel excel sebagai berikut:
Proses ini dapat diulang untuk pencarian akar ke 3 dan 4.
Menulis kode program
Setelah kita pahami algoritma Metode Muller di atas, saatnya menulis kode program. Berikut kode programnya.
//Menulis Identitas Program
/*
Program mencari akar polinomial dengan Metode Muller
Haruno Sajati, S.T., M.Eng.
Prodi Teknik Informatika
Sekolah Tinggi Teknologi Adisutipto
*/
//Deklarasi Header
#include<iostream.h>
#include<math.h>
//Fungsi Utama
void main()
{
//Deklarasi variabel
float koeff[10],koefg[10],x0,x1,x2,x3,error,fx0,fx1,fx2,a,b,c,d;
int j,k,iterasi;
//Inisialisasi persamaan
koeff[4]=1;
koeff[3]=2.8;
koeff[2]=-0.38;
koeff[1]=-6.3;
koeff[0]=-4.2;
for (k=4;k>=1;k--)
{
//Inisialisasi aproksimasi, error dan iterasi
x0=-0.5;
x1=0;
x2=0.5;
cout <<"Mencari akar ke : " << k << endl;
error=1;
iterasi=0;
//Lakukan perulangan jika error > toleransinya
while (error>0.00001)
{
//Mencari fx0, fx1 dan fx2
fx0=0;
for (j=4;j>=1;j--)
{
fx0=fx0+(koeff[j]*(pow(x0,j)));
}
fx0=fx0+koeff[0];
fx1=0;
for (j=4;j>=1;j--)
{
fx1=fx1+(koeff[j]*(pow(x1,j)));
}
fx1=fx1+koeff[0];
fx2=0;
for (j=4;j>=1;j--)
{
fx2=fx2+(koeff[j]*(pow(x2,j)));
}
fx2=fx2+koeff[0];
//Mencari koefisien a,b dan c persamaan fiting kuadrat
c=fx2;
b=(((x0-x2)*(x0-x2)*(fx1-fx2))-((x1-x2)*(x1-x2)*(fx0-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));
a=(((x1-x2)*(fx0-fx2))-((x0-x2)*(fx1-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));
d=(b*b)-(4*a*c);
//Mencari x3 (aproksimasi berikutnya
if (b<0)
{
x3=((-2*c)/(b-sqrt(d)))+x2;
}
else
{
x3=((-2*c)/(b+sqrt(d)))+x2;
}
//Mencari error
error=x3-x2;
if (error<0)
error*=-1;
//Perubahan aproksimasi
x0=x1;x1=x2;x2=x3;
iterasi++;
}
//Menampilkan output
cout << "Akar persamaan = " << x3 << endl;
cout << "Jumlah iterasi = " << iterasi << endl;
//Inisialisasi persamaan berikutnya
koefg[4]=0;
for(j=3;j>=0;j--)
{
koefg[j]=koeff[j+1]+(koefg[j+1]*x3);
}
for(j=4;j>=0;j--)
{
koeff[j]=koefg[j];
}
cout << "---------------------------------------" << endl;
}
}
Menjalankan Program
Berikut adalah eksekusi programnya:
Semoga bermanfaat


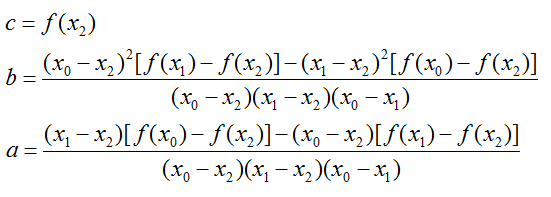






Semoga adik adik di STTA semakin pinter ..
Nitip link mas.. :)
anak sholeh
Boleh Suryono.. :)
itu aplikasinya apa?
Turbo C++ 4.5.
Great job for publishing such a beneficial web site. Your web log isn’t only useful but it is additionally really creative too. Mueller french press review