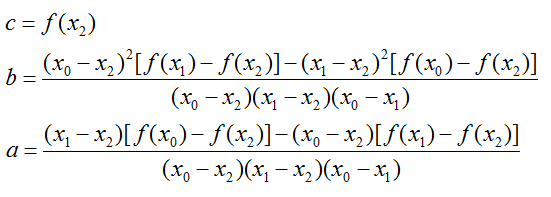Komputasi Numeris: Metode Muller (1)

Pendahuluan

Metode Muller diperkenalkan oleh David Eugene Muller (1924-2008), seorang profesor matematika dan computer science di University of Illinois.
Mirip dengan metode Newton yang sudah kita bahas sebelumnya di sini dan di sini,  Metode Muller digunakan untuk menyelesaikan sistem persamaan non linier. Berbeda dengan metode Newton, metode Muller tidak membutuhkan persamaan diferensial (turunan) dari persamaan yang akan dicari sehingga formula rumit seperti di bawah ini, tidak perlu dicari persamaan turunannya. Hore!


Metode Muller memiliki prinsip yang mirip dengan Metode Secant hanya saja berbeda dengan metode Secant yang memanfaatkan kurva fitting linear, metode Muller menggunakan kurva fitting berbentuk parabola. Inilah sebabnya berbeda dengan metode Secant yang hanya membutuhkan 2 nilai aproksimasi pembentuk kurva fitting linear, metode muller membutuhkan 3 nilai aproksimasi untuk membentuk kurva fitting parabolic.


Algortima
 
Untuk memahami metode Muller, perhatikan gambar di bawah ini:


Kita memiliki persamaan f(x) yang akan dicari akar persamaannya. Seperti pada metode-metode numeris yang lain, pertama kita tentukan nilai aproksimasi awal. Sesuai dengan yang dijelaskan sebelumnya, metode Muller membutuhkan 3 nilai aproksimasi awal (x0, x1 dan x2) misalnya -0.5, 0 dan 0.5.
Setelah ditentukan nilai x0, x1 dan x2, selanjutnya kita cari nilai f(x0), f(x1) dan f(x2). Jika mengacu pada contoh persamaan:
Persamaan ini memiliki grafik fungsi sebagai berikut:

maka:
f(-0.5) = -2.524232814
f(0.5) = 0.268980884
f(0) = -1

Berarti saat ini, kita sudah memiliki 3 titik sebagai "modal" pembentuk kurva fitting g(x) yaitu:

1. (x0, f(x0)) = (-0.5, -2.524232814)
2. (x1, f(x1)) = (0.5, 0.268980884)
3. (x2, f(x2)) = (0,-1)

Pertanyaan berikutnya adalah bagaimana persamaan parabola yang melewati 3 titik? Untuk menjawab pertanyaan ini, kita substitusikan saja tiga titik tersebut pada persamaan:
sehingga terbentuk tiga persamaan dengan tiga variabel. Persamaan yang terbentuk adalah:

1. -2.524232814 = 0.25a - 0.5b + c
2. 0.268980884 = 0.25a + 0.5b + c
3. -1 = c

Benar! Matriks!. Tiga persamaan dengan tiga variabel tersebut akan kita selesaikan dengan aturan Cramer Method dimana [1]:

sehingga nilai a, b, c berturut-turut adalah sebagai berikut:
a = -0.510503861
b = 2.793213698
c = -1

Sehingga persamaan kuadrat yang terbentuk adalah:
Setelah persamaan parabola g(x) ditemukan, saatnya mencari akar persamaan kuadrat dengan rumus:
Operator +/- ditentukan dari nilai b. Nilai x3 yang terbentuk adalah 0.385117564. Nilai ini akan menggeser x0, x1 dan x2 sebelumnya sehingga iterasi berikutnya x0=x1, x1=x2 dan x2=x3 atau x0=0, x1=-0.5 dan x2=0.385117564.
Perhatikan tabel excel berikut:
Setelah iterasi ke 3 nilai x3 telah "stabil" sehingga dapat dikatakan persamaan tersebut telah ditemukan akarnya.

Listing Program

Setelah kita pahami algoritma metode Muller tersebut, saatnya kita menulis kode programnya:
/*
Program mencari akar persamaan non linear
Menggunakan Metode Muller
Haruno Sajati, S.T., M.Eng.
Program Studi Teknik Informatika
Sekolah Tinggi Teknologi Adisutjipto
*/

//Deklarasi Header
#include<iostream.h>
#include<math.h>

//Fungsi Utama
void main()
{
  //Deklarasi Variabel
  float x0,x1,x2,x3,fx0,fx1,fx2,a,b,c,d,error;
  int iterasi;

  //inisialisasi nilai awal aproksimasi
  x0=-0.5;
  x1=0;
  x2=0.5;

  error=1;
  iterasi=0;

  //Proses diulang selama error > toleransi
  while (error>0.00001)
  {
        fx0 = 4*sin(x0)-pow(2.718282,x0);
        fx1 = 4*sin(x1)-pow(2.718282,x1);
        fx2 = 4*sin(x2)-pow(2.718282,x2);

        c=fx2;
        b=(((x0-x2)*(x0-x2)*(fx1-fx2))-((x1-x2)*(x1-x2)*(fx0-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));
        a=(((x1-x2)*(fx0-fx2))-((x0-x2)*(fx1-fx2)))/((x0-x2)*(x1-x2)*(x0-x1));

        d=(b*b)-(4*a*c);

        if (b<0)
        {
            x3=((-2*c)/(b-sqrt(d)))+x2;
        }
        else
        {
            x3=((-2*c)/(b+sqrt(d)))+x2;
        }

        //Mencari error
        error=x3-x2;
        if (error<0)
        {
            error*=-1;
        }

        //Mencari aproksimasi berikutnya
        x0=x1;x1=x2;x2=x3;

        //Menghitung jumlah iterasi dan proteksi infinit loop
        iterasi++;
        if (iterasi > 40)
        {
            cout << "Gagal ditemukan akarnya" << endl;
            break;
        }
  }

  //Menampilkan hasil
  cout << "Akar persamaan = " << x3 << endl;
  cout << "Jumlah iterasi = " << iterasi << endl;

}

Tampilan Eksekusi Program

Akar berikutnya silahkan dibaca di sini (Metode Muller dengan Deret Taylor)
Semoga bermanfaat

Daftar Pustaka

[1] Komputasi Numeris: Teori dan Aplikasi, P. Buyung Kosasih, Penerbit Andi, Yogyakarta, 2006